5.8 Un per pensar-hi. $L\wedge M\Rightarrow\neg P,\ I\Rightarrow P,\ M,\ I\vdash\neg L$

Intenta fer 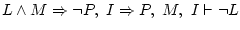$L\wedge M\Rightarrow\neg P,\ I\Rightarrow P,\ M,\ I\vdash\neg L$ de cap; després escriu-lo en paper. Queda:

$$\begin{fitch} \par L \wedge M \Rightarrow \neg P \\ \par I \... ...tarrow$\ 2,4 \\ \par \neg L & I$\neg$\ 5,7,8 \par \end{fitch}$$

L'expresso per paraules: ``si uses Linux i Mozilla com a navegador, t'evites els problemes. En canvi, si uses Internet Explorer tindràs problemes. Ara tu uses Mozilla, però també Internet Explorer a vegades. Per tant, sé que no uses Linux''.

Potser sembla evident: ``és clar, perquè IE no està en Linux'', però fixa't que no he dit això en cap moment. No hi surt el $I\Rightarrow\neg L$ enlloc.

La forma en què hauries de pensar mentre prepares l'exercici és:

1. Necessito demostrar $\neg L$, que és la negació d'alguna cosa. No es veu cap regla de la forma quelcom implica $\neg L$ que em permeti obtenir-ho directament. S'haurà de fer d'una altra forma, per exemple amb la introducció de la negació (reducció a l'absurd): suposem que sí que uso Linux.
2. En el cas de que usés Linux, usaria Linux i Mozilla, perquè ja usava Mozilla abans (és la tercera veritat que hi surt escrita a l'enunciat).
3. En usar Linux i Mozilla, no tindria problemes informàtics, perquè $L\wedge M\Rightarrow\neg P$.
4. Però també usava Internet Explorer (quarta veritat), i com que IE genera problemes, jo tindré problemes. $P$.
5. He arribat a una contradicció: $\neg P$ i $P$. Per tant, el que passa és que la suposició que he fet de que uso Linux és incorrecta: resulta que $\neg L$.

Doncs ara només s'ha de seguir el mateix procediment, però escrivint-ho pas per pas i usant les regles. S'obtindrà la mateixa figura que surt a dalt, que casualment té 5 línies de procediment (les 4 primeres són només per copiar les veritats). Cada línia es correspon amb els passos que he explicat aquí.