5.8 One to think. $L\wedge M\Rightarrow\neg P,\ I\Rightarrow P,\ M,\ I\vdash\neg L$

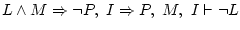Try $L\wedge M\Rightarrow\neg P,\ I\Rightarrow P,\ M,\ I\vdash\neg L$ only thinking; then write it down on paper. It's something like:

$$\begin{fitch} \par L \wedge M \Rightarrow \neg P \\ \par I \... ...tarrow$\ 2,4 \\ \par \neg L & I$\neg$\ 5,7,8 \par \end{fitch}$$

I will put it by words: ``if you use Linux and Mozilla as a browser, you avoid problems. In contrast, if you use Internet Explorer you will have problems. Now you use Mozilla, but also Internet Explorer sometimes. Consequently, I know that you don't use Linux''.

Maybe that seems evident: ``of course, since IE is not on Linux'', but notice that I never said that. There isn't the $I\Rightarrow\neg L$ anywhere.

The way in which you should think when you prepare this exercise is:

1. I need to prove$\neg L$, which is the negation of something. It can't be seen any rule of the form something implies $\neg L$ which allows me to obtain it directly. We should think of another way, for example negation introduction (reduction to the absurd): suppose that I do use Linux.
2. In the case when I use Linux, I would use both Linux and Mozilla, since I already used Mozilla before (it's the third truth which is written in the original problem).
3. Using both Linux and Mozilla, I wouldn't have computer problems, since $L\wedge M\Rightarrow\neg P$.
4. But I also used Internet Explorer (fourth truth), and since IE generates problems, I will have problems. $P$.
5. I got a contradiction: $\neg P$ and $P$. So, what's happening is that the supposition I did of using Linux is wrong: actually, $\neg L$.

Now you just have to follow the same procedure, but writing down each step, and using the derivation rules. What you will obtain is the figure above, which happens to have 5 procedure lines (the first 4 are only to copy the truths). Each line corresponds with the steps given here.