5.8 Uno para pensar. $L\wedge M\Rightarrow\neg P,\ I\Rightarrow P,\ M,\ I\vdash\neg L$

Intenta hacer 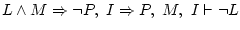$L\wedge M\Rightarrow\neg P,\ I\Rightarrow P,\ M,\ I\vdash\neg L$ de cabeza; luego escríbelo en papel. Queda:

$$\begin{fitch} \par L \wedge M \Rightarrow \neg P \\ \par I \... ...tarrow$\ 2,4 \\ \par \neg L & I$\neg$\ 5,7,8 \par \end{fitch}$$

Lo pongo con palabras: ``si usas Linux y Mozilla como navegador, te evitas los problemas. En cambio, si usas Internet Explorer tendrás problemas. Ahora tú usas Mozilla, pero también Internet Explorer a veces. Por lo tanto, sé que no usas Linux''.

A lo mejor te parece evidente: ``claro, porque IE no está en Linux'', pero fíjate en que el $I\Rightarrow\neg L$ no sale por ningún lado.

La forma en que deberías pensar mientras preparas el ejercicio es:

1. Necesito demostrar $\neg L$, que es la negación de algo. No se ve ninguna regla de la forma algo implica $\neg L$ que me permita obtenerlo directamente. Habrá que usar otra forma, por ejemplo la introducción de la negación (reducción al absurdo): supongamos que sí que uso Linux.
2. En el caso de que uso Linux, usaría Linux y Mozilla, porque ya usaba Mozilla antes (es la tercera verdad que hay escrita en el enunciado).
3. Al usar Linux y Mozilla, no tendría problemas informáticos, porque $L\wedge M\Rightarrow\neg P$.
4. Pero también usaba Internet Explorer (cuarta verdad), y como IE genera problemas, yo tendré problemas. $P$.
5. He llegado a una contradicción: $\neg P$ y $P$. Por lo tanto, lo que pasa es que la suposición que he hecho de que uso Linux es incorrecta: resulta que $\neg L$.

Pues ahora sólo hay que seguir el mismo procedimiento, pero escribiéndolo paso por paso y usando las reglas. Lo que se obtiene es la figura que sale arriba, que casualmente tiene 5 líneas de procedimiento (las 4 primeras son sólo para copiar las verdades). Cada línea se corresponde con los pasos que he explicado aquí.